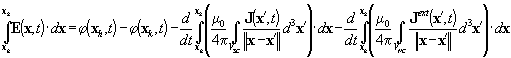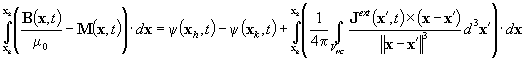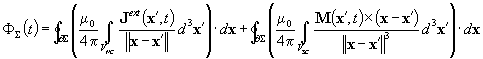Elettrodinamica
degli elementi superconduttivi massicci
La
determinazione delle distribuzioni di corrente, campo magnetico e perdite in
alternata all’interno di un corpo superconduttivo costituisce un requisito
essenziale per il progetto di dispositivi di interesse industriale. Per questa
ragione presso il Laboratorio di Superconduttività si sono sviluppati modelli
numerici per il calcolo di tali distribuzioni in corpi superconduttivi
soggetti alle condizioni di funzionamento più ricorrenti nella pratica. In
particolari sono stati sviluppati i seguenti modelli:
1.
Modello per il calcolo delle distribuzioni di corrente e AC losses
all’interno di corpi superconduttivi soggetti a corrente di trasporto e
campo magnetico esterno variabili nel tempo
2.
Modello per l’analisi del processo di magnetizzazione di corpi
superconduttivi soggetti a campo magnetico esterno
3.
Modello per il calcolo delle distribuzioni di corrente e AC losses
all’interno di corpi superconduttivi posti in vicinanza di corpi
magnetizzabili e soggetti al campo magnetico prodotto da una bobina
interagente con un circuito esterno
1.
Modello per il calcolo delle distribuzioni di corrente e AC losses
all’interno di corpi superconduttivi soggetti a corrente di trasporto e
campo magnetico esterno variabili nel tempo
|
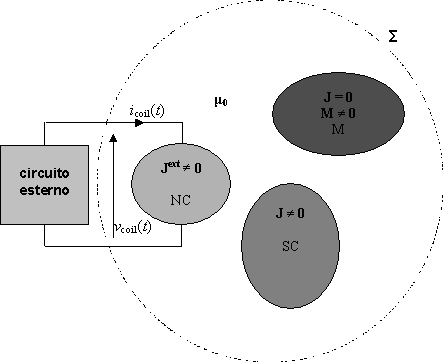
Si
consideri un sistema costituito da un corpo superconduttivo (SC) soggetto ad
una corrente di trasporto assegnata e posto sotto l’influenza del campo
magnetico generato dalle correnti circolanti in un corpo conduttivo normale
(bobina in rame, NC) presente in vicinanza (figura 1.1). Tali correnti sono
assunte note, ed è noto pertanto il potenziale vettore da esse generato in
ogni punto dello spazio. Come relazione costitutiva del materiale
superconduttore si assume la legge della potenza tre i vettori E e J.
|
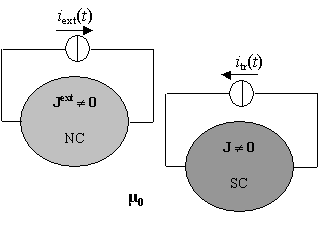
figura 1.1
|
Il
volume occupato dal corpo superconduttivo viene suddiviso in un numero finito
di elementi tridimensionale. La densità di corrente all’interno di ogni
elemento viene assunta uniforme, ed il suo valore viene espresso in funzione
delle correnti attraverso le facce dell’elemento considerato mediante la
tecnica dei minimi quadrati, i.e.
|
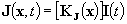
|
(1.1)
|
dove
KJ è una matrice che varia da elemento a elemento (uniforme
in ogni elemento) e I è il vettore delle correnti attraverso tutte le
facce della discretizzazione adottata.
Introducendo
il potenziale vettore magnetico A e il potenziale elettrico scalare
φ è possibile esprimere l’integrale di linea del campo elettrico su
ogni percorso congiungente i centri xh e xk
di due elementi confinanti attraverso la seguente relazione
|
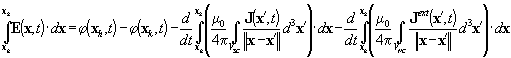
|
(2.1)
|
Sostituendo
al suo interno l’equazione (1.1) e la relazione costitutiva del materiale
superconduttore la precedente equazione può essere interpretata come
l’equazione delle tensioni di un ramo di circuito elettrico contenete dei
termini di auto/mutua induzione associati alle correnti della regione SC, un
termine resistivo non lineare associato al campo elettrico ed un termine di
tensione impressa associato alla derivata delle correnti della regione
normale.
|
Ne consegue che l’intera
regione superconduttiva può essere schematizzata mediante un circuito avente come numero di nodi il numero di
elementi in cui è stato suddiviso il volume da essa occupato, aumentato di
due per prevedere la connessione ad un generatore di corrente esterno e come
numero di rami il numero di facce attraversate da corrente. Nella figura 2.1 è riportata una cella elementare, relativa ad un elemento di contorno,
della rete elettrica equivalente ottenuta da una discretizzazione del volume
SC mediante prismi a base triangolare.
La
soluzione della rete elettrica può essere effettuata mediante tecniche
circuitali standard una volta che i suoi paramenti sono stati definiti, e
consente di ricostruire, tramite l’equazione (1.1) e la relazione d
costitutiva, la distribuzione di corrente e di perdite AC all’interno del
volume SC considerato.
|
figura 2.1
: Cella elementare della rete elettrica equivalente relativa ad un elemento
di contorno
|
Il
modello di calcolo fin qui esposto non è applicabile quando il volume
occupato dal superconduttore non è omogeneo. Tuttavia nella pratica gli
elementi superconduttivi compositi sono molto ricorrenti; ad esempio uno
strand superconduttivo multifilamentare col quale si realizzano i cavi SC per
magneti, è realizzato mediante un elevato numero di filamenti superconduttivi
di piccola sezione,
immersi in una matrice di materiale conduttore normale (rame). Con riferimento
a questa struttura è ancora possibile utilizzare il modello sviluppato se si
definisce, mediante un processo di media su un volume piccolo rispetto alle
dimensioni totali dello strand ma sufficientemente grande da contenere un
elevato numero di filamenti superconduttivi e di zone in rame, una relazione E=E(J,x)
valida in ogni punto, indipendentemente dal materiale (superconduttore o rame)
in esso presente. A causa del twisting dei filamenti, la caratteristica
equivalente è esplicitamente dipendente dal punto.
Il
modello sviluppato è stato validato prendendo in esame alcuni benchmarks
per cui sono disponibili delle soluzioni analitiche. Di seguito sono riportati
i confronti tra risultati numerici e analitici per i casi analizzati.
|
Caso
I: filo conduttore normale, conducibilità σ = 3.07 109
S/m, raggio r = 1 mm, lunghezza l = 1 m, soggetto a corrente di
trasporto sinusoidale con valore efficace 10 A e frequenza 250 Hz
|
|
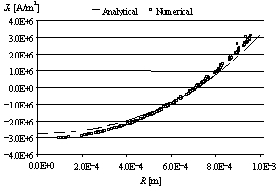
|

|
|
distribuzione
di densità di corrente (componente assiale) nella sezione centrale
all’istante t = 2 ms
|
andamento
della potenza dissipata all’interno del filo durante i primi due
periodi
|
|
Caso
II: filo conduttore normale, conducibilità σ = 3.07 106
S/m, raggio r = 1 mm, lunghezza l = 1 m, soggetto a campo magnetico
assiale uniforme sinusoidale con valore efficace 1 T e frequenza 250 Hz
|
|
|
|
|
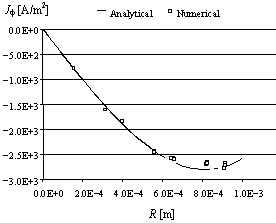
distribuzione
di densità di corrente (componente azimutale) nella sezione centrale
all’istante t = 9 ms
|
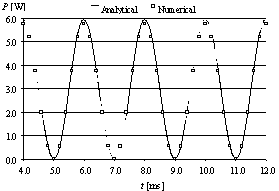
andamento
della potenza dissipata all’interno del filo durante i primi due
periodi
|
|
Caso
III: filo superconduttore, raggio r = 1 mm, lunghezza l = 1 m, soggetto
a corrente di trasporto variabile con legge itr(t)=K[(1-t/t0)-1/N-1]N/(N-1),
con K = 2218 A, N = 6 , t0 = 1 s
|
|
|
|
|
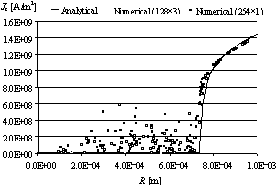
distribuzione
di densità di corrente (componente assiale) nella sezione centrale
all’istante t = 0.97 s
|
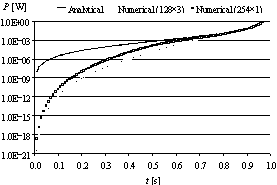
andamento
della potenza dissipata all’interno del filo nell’intervallo 0 s -
1 s
|
Occorre
evidenziare che il modello descritto è indipendente dalla temperatura; si
suppone cioè che, in ogni istante, l’intero volume SC sia in equilibrio
termico a temperatura assegnata.
2.
Modello per l’analisi del processo di magnetizzazione di corpi
superconduttivi soggetti a campo magnetico esterno
Tipicamente
la relazione costitutiva di un materiale superconduttore è espressa mediate
una relazione non lineare tra i vettori E e J, che conduce ad un
comportamento isteretico nella caratteristica M -
B in ogni punto calcolata in fase di post-processing.
In questo modello si segue un approccio differente: la caratteristica
isteretica M -
B è assunta direttamente come relazione costitutiva del materiale SC,
che è quindi schematizzato come un materiale magnetizzabile con conducibilità
elettrica nulla. La dipendenza locale tra i vettori M e B è
espressa attraverso un modello fenomenologico vettoriale di isteresi del tipo
Duhem. La principale caratteristica di questo modello è l’accoppiamento di
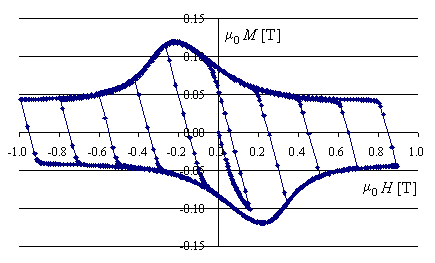
due modelli isteretici, uno per le ampiezze e uno per le direzioni. Nella
figura 1.2 è riportata, a titolo di esempio, l’evoluzione isteretica della
magnetizzazione calcolata nel caso di campo magnetico oscillante con ampiezza
lentamente crescente.
|
|
|
figura.
1.2 andamento isteretico di m0
M in funzione di m0
H.
|
Si
consideri un sistema costituito da corpi conduttori normali (bobine in rame,
NC) e corpi superconduttori (SC) immersi nel vuoto.
|
Il
volume occupato dal corpo superconduttivo viene suddiviso in un numero finito
di elementi tridimensionale. L’induzione magnetica all’interno di ogni
elemento viene assunta uniforme, ed il suo valore viene espresso in funzione
dei flussi attraverso le facce dell’elemento considerato mediante la tecnica
dei minimi quadrati, i.e.
|
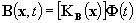
|
(1.2)
|
dove
KB è una matrice che varia da elemento a elemento (uniforme
in ogni elemento) e Φ è il vettore dei flussi attraverso tutte le
facce della discretizzazione adottata.
|
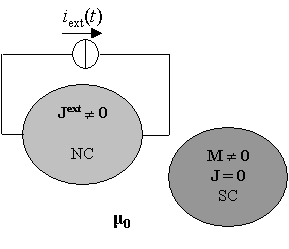
figura. 2.2
|
Il
campo magnetico totale H in ogni punto si può esprimere come somma di
un campo magnetico HJ, associato alle correnti Jext
che circolano nelle bobine in rame, e un campo HM, associato
alla distribuzione di magnetizzazione M presente nella regione
superconduttiva. Introducendo, relativamente alla componente HM,
il potenziale scalare magnetico Ψ è possibile esprimere l’integrale di
linea del campo magnetico su ogni percorso congiungente i centri xh
e xk di due elementi confinanti attraverso la seguente
relazione
|
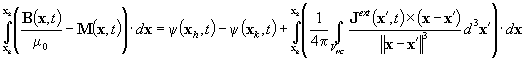
|
(2.2)
|
Sostituendo
al suo interno l’equazione (1.2) e la relazione costitutiva del materiale
superconduttore la precedente equazione può essere interpretata come
l’equazione di bilancio delle forze magnetomotrici di un ramo di circuito
magnetico contenete un termine di riluttanza lineare e uno non lineare
associati ai flussi della regione SC e un termine di forza magnetomotrice
impressa associato alle correnti della regione normale.
Il
flusso magnetico attraverso una generica faccia Sj
posta sul contorno del dominio SC può essere espresso attraverso la seguente
relazione
|
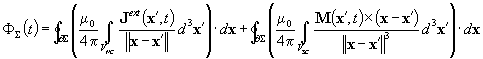
|
(3.2)
|
Tale
relazione permette di interpretare il flusso attraverso ogni faccia esterna
come risultante dal parallelo tra un generatore di flusso indipendente e uno
controllato, connessi al centro dell’elemento a cui la faccia di contorno
appartiene e ad un nodo esterno fittizio.
|
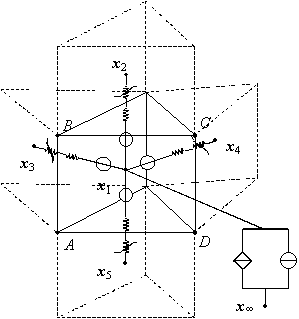
figura 3.2: Cella elementare della rete magnetica equivalente relativa ad un elemento
di contorno
|
Essi rappresentano il contributo
delle linee di campo di induzione magnetica associate alle correnti esterne e
alla magnetizzazione rispettivamente, che si richiudono all’infinito
attraversando la faccia Sj.
Ne consegue
che l’intero corpo superconduttivo può essere schematizzato mediante un
circuito magnetico avente come numero di nodi il numero di elementi in cui è
stato suddiviso il volume da esso occupato e come numero di rami il numero di
facce. Nella figura 3.2 è riportata una cella elementare, relativa ad un
elemento di contorno, della rete magnetica equivalente ottenuta da una
discretizzazione del volume SC mediante prismi a base triangolare.
La
soluzione della rete magnetica può essere effettuata mediante tecniche
circuitali standard una volta che i suoi paramenti sono stati definiti, e
consente di ricostruire, tramite l’equazione (2.1) e la relazione
costitutiva, la distribuzione di campo magnetico e magnetizzazione
all’interno del volume SC considerato.
|
Inoltre, in fase di post-processing,
a partire dalla distribuzione di magnetizzazione all’interno del volume SC,
è possibile ricostruire il contributo al campo magnetico in tutto lo spazio
prodotto dall’elemento superconduttivo.
Occorre
evidenziare che il modello descritto è indipendente dalla temperatura; si
suppone cioè che, in ogni istante, l’intero volume SC sia in equilibrio
termico a temperatura assegnata.
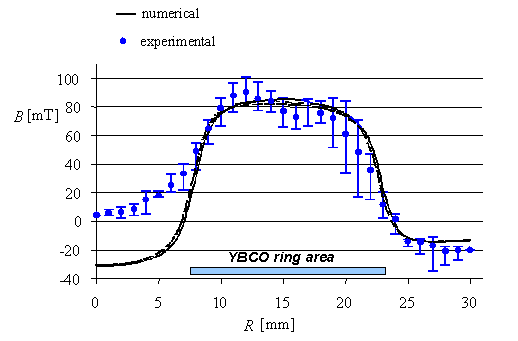
Il
modello numerico descritto è stato adoperato nell’analisi del processo di
magnetizzazione impulsata di anelli di YBCO raffreddati in assenza di campo
magnetico. Il confronto tra risultati numerici e sperimentali è mostrato in
figura 4.2
|
|
|
figura 4.2:
Profilo della componente assiale dell’induzione magnetica intrappolata
ad 1 mm di distanza dalla superficie superiore di un anello
superconduttivo soggetto ad un impulso di campo assiale
|
I
risultati ottenuti per via numerica sono in buon accordo con quelli rilevati
sperimentalmente per quanto riguarda il campo intrappolato nella regione posta
sopra agli anelli SC, mentre una minore rispondenza si riscontra nei valori di
campo intrappolato nella parte centrale dei provini. Questi risultati sono
complementari a quelli ottenuti adottando la legge della potenza come
caratteristica costitutiva del materiale SC, che, al contrario, riproducono un
andamento di campo che nella zona centrale è in buon accordo coi risultati
sperimentali mentre si discosta notevolmente sulla superficie del provino.
Tale considerazione induce a ritenere che una più accurata modellizzazione
del processo di magnetizzazione si possa ottenere schematizzando il materiale
come corpo sia conduttivo che magnetizzabile.
3.
Modello per il calcolo delle distribuzioni di corrente e AC losses
all’interno di corpi superconduttivi posti in vicinanza di corpi
magnetizzabili e soggetti al campo magnetico prodotto da una bobina
interagente con un circuito esterno
Si
consideri un sistema costituito da un corpo superconduttivo (SC) posto in
vicinanza di un corpo magnetizzabile (M) e soggetto all’influenza del campo
magnetico prodotto da un bobina normale (NC) interagente con un circuito
esterno (figura 1.3). Come relazione costitutiva del materiale superconduttore
si assume la legge della potenza tre i vettori E e J. Per la
regione magnetizzabile invece, la relazione locale M – B, nel
più generale dei casi non lineare e isteretica, è assunta come legge
costitutiva del materiale. La resistività è assunta infinita, ossia si
trascura il contributo al campo delle correnti in essa indotte.
|
|
|
figura 1.3
|
Sia la regione
superconduttiva che quella magnetizzabile sono suddivise in un numero finito
di elementi tridimensionale. Applicando alla regione superconduttiva la
procedura di derivazione del circuito elettrico equivalente e alla regione
magnetizzabile la procedura di derivazione del circuito magnetico equivalente
descritte sopra, è possibile schematizzare l’intero sistema di figura 1.3
attraverso una rete elettrica e una rete magnetica accoppiate. La rete
elettrica conterrà termini forzanti associati ai flussi della rete magnetica
e, allo stesso modo, la rete magnetica conterrà termini forzanti associati
alla correnti della rete elettrica. Nel caso di mezzi magnetizzabili lineari
è possibile ricavare esplicitamente l’espressione dei flussi nella regione
M in funzione delle correnti nella regione SC e delle corrente nella bobina ed
incorporare i termini forzanti della rete elettrica associati ai flussi
all’interno dei termini di auto e mutua induzione. Se l’ipotesi di
linearità dei mezzi magnetici non sussiste tale procedura non è applicabile
e i sistemi risolventi delle due reti non sono disaccoppiabili.
Siccome nel caso in esame
la corrente che circola all’interno della bobina non è una quantità nota,
i sistemi risolventi delle reti elettrica e magnetica risultano indeterminati.
Per rimuovere questa indeterminazione è possibile utilizzare l’equazione di
bilancio delle tensioni del circuito elettrico esterno al quale la bobina è
connessa. Infatti, applicando il teorema di Poynting alla superficie chiusa
Σ di figura è possibile esprimere la tensione ai capi della bobina in
funzione delle correnti e dei flussi nel seguente modo
|
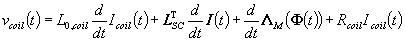
|
(1.3)
|
dove L0,coil
è il coefficiente di autoinduzione della bobina in assenza di corpi
magnetizzabili, LSC è un vettore costante che
moltiplica scalarmene il vettore delle correnti della regione superconduttiva,
ΛM è una funzione dei flussi della regione magnetizzabile che
diviene lineare nel caso di mezzi magnetici lineari e Rcoil
rappresenta la resistenza della bobina.
Il
modello numerico descritto è stato adoperato per calcolare la corrente di
guasto in un circuito nel quale è inserito un limitatore di corrente
superconduttivo di tipo induttivo. Il confronto tra risultati numerici e
sperimentali è mostrato in figura 2.3
|
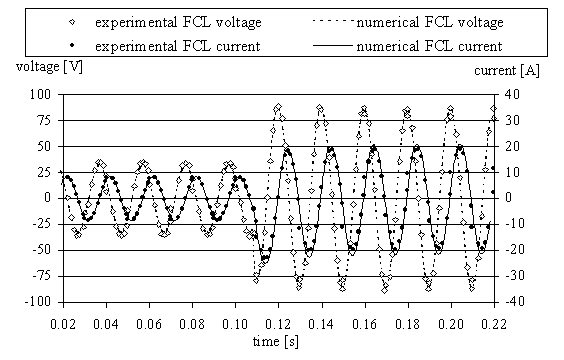
|
|
figura 4.2:
corrente e tensione ai capi del limitatore di corrente durante un guasto
|
I risultati ottenuti per
via numerica sono in buon accordo con quelli rilevati sperimentalmente,
soprattutto per quanto concerne la fase di normale funzionamento e i primi
istanti dopo l’evento del guasto.